戴森球计划太阳帆弹射器部署方法 太阳帆发射指南

二、射击目标点

太阳帆射击的目标点在轨道上不是固定的，取决于两个因素：太阳帆轨道面法向和弹射器的全局坐标。

目标点一定在轨道上，其方向是轨道面法向与弹射器位置向量的向量积。

好了知道这句话后面的就不用看了 下面分别解释两个因素。

1.太阳帆轨道面法向

太阳帆轨道的轨道倾角θ(0°≤θ≤180°)和升交角经度η(0°≤η≤360°)决定了轨道面的法线方向。

游戏预置的1号轨道倾角0°、升交角经度0°，其法向就是z轴正向(0,0,1)。玩家自定义的轨道法向按如下方式确定：

先将向量(0,0,1)绕x轴旋转θ，再绕z轴旋转η

因此轨道面法向n=(sinθsinη，-sinθcosη，cosθ)。

推导过程

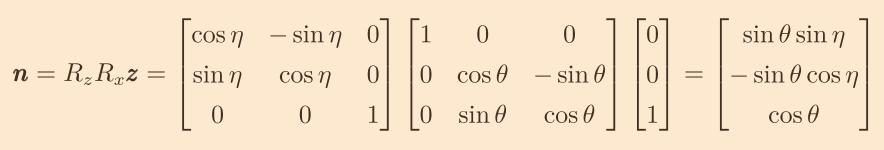
2.弹射器的全局坐标

因为弹射器在行星上，首先需要确定的是行星坐标，行星位置由行星在轨道上的相位ω(ω=2πt/T，T为公转周期，t为当前时刻)、公转轨道倾角λ、公转轨道与黄道平面交点的经度μ、行星轨道的半径r决定。

行星坐标P=r(cosμcosω-cosλsinμsinω，sinμcosω+cosλcosμsinω，sinλsinω)

推导过程

而弹射器在行星上的坐标则与弹射器所在纬度α(南纬为负，北纬为正)、天球经度2πt/K+β= kω+β(*)(K为自转周期，k=T/K是行星公转周期与自转周期之比，如果反向自转则k=-T/K)、行星的地轴偏角γ、行星自身的半径a有关。

(*)β是初始时刻弹射器经度与x轴的经度差(向东增加)，虽然β一般很难确定，但问题其实不大。如果行星不是轨道共振星，那么β可以忽略，因为往往K远小于T，可以认为一个昼夜间行星位置没变，但天球经度已经取遍0~360°，β带来的影响很小。潮汐锁定星的β则非常好确定：可以认为正是其子夜经线(永夜面中心经线)的经度。

实际上在游戏里弹射器自身的高度对这个坐标也是有影响的，但是因为量级太小这里不考虑。

所以弹射器在行星自身的局部坐标系上的坐标为(r(cosμcosω-cosλsinμsinω)+a(cosαcosγcos(kω+β)+sinαsinγ)，r(sinμcosω+cosλcosμsinω)+a cosαsin(kω+β)，rsinλsinω+a(sinαcosγ-cosαsinγcos(kω+β)))。 开始头大

目标点T的位置满足OT=n×OE/| n×OE |*R，R为太阳帆轨道的半径。

关于它的形式我已经找到一个让人脑疼的表达式，可惜这里的空白写不下。

你们一定不会想和这种形式的表达式打交道

复杂的表达式预示着这个问题的高精度的定量解只能通过程序为每个玩家的场景去算(暗示MOD)，我们在这里必须简化一下。